Studio Pyraxis - Wattle and Daub Renderman Tutorial

Wattle and Daub
Procedural Basketweave Shader
(return to Studio Pyraxis)

Tutorial

The math used in this shader template is limited to Pythagoras' theorum for finding the hypoteneuse of a triangle (a²+b²=c²), and the cosine curve.

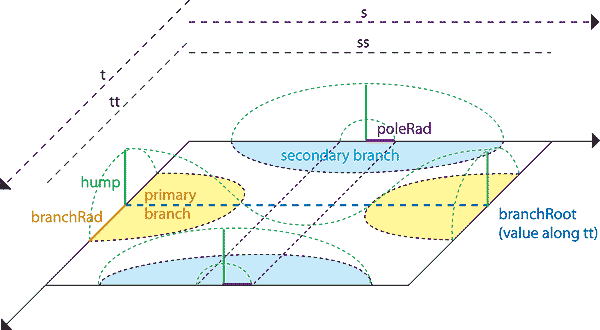
To define the displacement of the basketweave, mod() is used to divide the 0 to 1 ranges of s and t into a user-defined number of blocks. Within each block, ss and tt will range from 0 to 1. The number of blocks will be represented in the user controls as Sections (numSections, along s) and Branches (numBranches, along t). From now on, only ss and tt will be used in the calculation of the branch displacement.

float ss = mod(s * numSections, 1),
tt = mod(t * numBranches, 1);

To start, the branches are defined as a stripe running through the center of each tt block. The width of the stripe is defined by branchRad. BranchRoot is by default 0.5 (halfway down the block) but could easily be changed if desired.

float branchRoot = 0.5,
branchRad = 0.25;
if (tt > (branchRoot - branchRad) && tt < (branchRoot + branchRad))
{
hump = 1;
}

However this formula will only give half the number of branches needed. A second row of branches will be added that uses 0 and 1 as its root instead of branchRoot. But since the branches overlap along tt with radii over 0.25, there isn't any point adding a second row until we've defined the curvature of the first row.

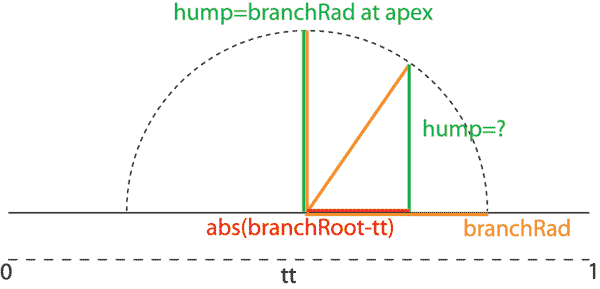
Here is a cross section of a branch. Hump at its highest point (the middle of a branch) is equal to the radius of the branch. Pythagoras' theorum can be used to find the hump for any other value of the base of the triangle. Since the branch radius remains constant, the branch will form a perfect half-circle.

float branchRoot = 0.5,
branchRad = 0.25;
if (tt > (branchRoot - branchRad) && tt < (branchRoot + branchRad))
{
hump = sqrt(abs(branchRad*branchRad - (branchRoot-tt)*(branchRoot-tt)))/branchRad;
}

Remember that depending on the number of branches, the aspect ratio of hump to tt will change, so the branch may not always appear perfectly round at rendertime. This can be resolved by multiplying hump by a user-defined constant at the end of the shader, so that a branch can be as flat or as tall as the user wants.

At this point the second, interleaved row of branches can be added by offsetting them along tt by 0.5 before the final hump value is calculated.

/* if we're within the area of a primary branch */
if (tt > (branchRoot - branchRad) && tt < (branchRoot + branchRad))
{
hump = sqrt(abs(branchRad*branchRad - (branchRoot-tt)*(branchRoot-tt)))/branchRad; /* roundness */
}
/* if we're within the area of a secondary branch */
if ((tt < branchRad) || (tt > (1 - branchRad)))
{
tt = abs(tt-0.5) ; /* because this row is secondary, offset the branches along t */
hump = sqrt(abs(branchRad*branchRad - (tt-branchRoot)*(tt-branchRoot)))/branchRad; /* roundness */
}

Here's where it gets more complicated. The branches need to appear to weave in and out of each other, without losing their curvature. This can be done by multiplying the hump value by a modified cosine wave along ss. I found that a cosine wave alone would push the branch too far through the "wattle" (hump=0 surface). It is also necessary to use 1-cosine so that the branch dips in the center instead of rising.

Next, the poles are added. They are built basically the same way as the branches, but using ss instead of tt. Again, it's necessary to multiply by a constant so that the branches appear to be woven over and under the poles instead of penetrating them, as they would if the pole radius was the same as a branch radius.

/* if we're within the area of a primary pole */
if (ss > (poleRoot - poleRad) && ss < (poleRoot + poleRad))
{
temp = sqrt(abs(poleRad*poleRad - (poleRoot-ss)*(poleRoot-ss)))/poleRad; /* roundness */
temp = temp * poleRad * 3 ; /* manually increase height cause km, s, radius don't match */
if (temp > hump) hump = temp;
}
/* if we're within the area of a secondary pole */
if ((ss < poleRad) || (ss > (1 - poleRad)))
{
ss = abs(ss-0.5) ;
temp = sqrt(abs(poleRad*poleRad - (ss-poleRoot)*(ss-poleRoot)))/poleRad; /* roundness */
temp = temp * poleRad * 3 ;
if (temp > hump) hump = temp;
}

Last, some randomness is added to the radii of the branches (before anything else is calculated) to give a more organic, less mechanical look. The randomness factor pulls in user variables and then applies noise to them based on the value along s or t. If ss and tt were used instead, each branch would have identical distortion.

float branchRad = userBranchRad + (((noise(s*branchRadVarianceS, t*branchRadVarianceS)-0.5)*2)*branchRadVarianceT);
float poleRad = userPoleRad + (((noise(s*poleRadVarianceS, t*poleRadVarianceS)-0.5)*2)*poleRadVarianceT);

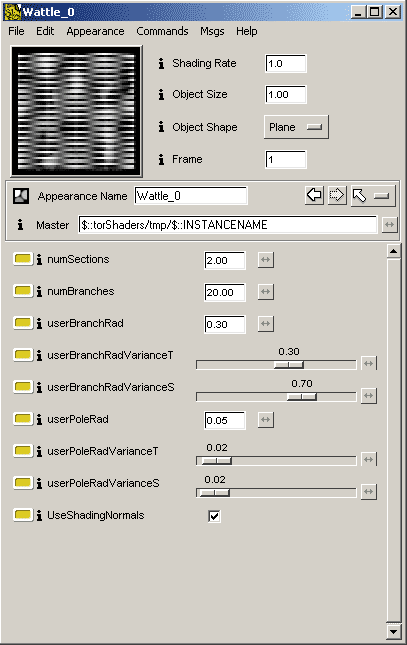
The finished shader template. The float node can be further modified in SLIM to add bumps and irregularities along the branches, wood grain pattern, etc.

Shader Template in SLIM

Complete Shader Code

displacement
wattle(float Km = 0.2, /* displacement magnitude */
numSections = 2, /* [1 50] number of sections along s */
numBranches = 2, /* [1 50] number of branches along t */
userBranchRad = 0.3, /* [0.00001 0.5] mean radius of each branch */
userBranchRadVarianceT = 0.5, /* [0 0.5] range within which branch rad varies */
userBranchRadVarianceS = 0.5, /* [0 1] range within which branch rad varies */
userPoleRad = 0.1, /* [0.00001 0.5] mean radius of each branch */
userPoleRadVarianceT = 0.15, /* [0 0.5] range within which pole rad varies */
userPoleRadVarianceS = 0.15, /* [0 1] range within which pole rad varies */
UseShadingNormals = 1 /* [0 or 1] */)
{
/* default variable declarations */
float hump = 0;
vector diff = normalize(N) - normalize(Ng);

/* custom variable declarations */
float temp = 0;
float ss = mod(s * numSections, 1),
tt = mod(t * numBranches, 1);
float branchRoot = 0.5,
poleRoot = 0.5;

/* conversion of variables in convenient user scale to actual scale, may need adjustment */
float branchRadVarianceS = userBranchRadVarianceS*10 ;
float branchRadVarianceT = userBranchRadVarianceT ;
float poleRadVarianceS = userPoleRadVarianceS*10 ;
float poleRadVarianceT = userPoleRadVarianceT ;

/* randomize user inputs */
float branchRad = userBranchRad + (((noise(s*branchRadVarianceS, t*branchRadVarianceS)-0.5)*2)*branchRadVarianceT);
float poleRad = userPoleRad + (((noise(s*poleRadVarianceS, t*poleRadVarianceS)-0.5)*2)*poleRadVarianceT);

/* STEP 1 - make a copy of the surface normal one unit in length */
normal n = normalize(N);

/* STEP 2 - calculate an appropriate value for the displacement */

/* if we're within the area of a primary branch */
if (tt > (branchRoot - branchRad) && tt < (branchRoot + branchRad))
{
temp = sqrt(abs(branchRad*branchRad - (branchRoot-tt)*(branchRoot-tt)))/branchRad; /* roundness */
temp = temp - ((1-cos(ss*2*PI)*((1+poleRad)/2))-(-0.5*poleRad+0.5)) ; /* interleave */
if (temp > hump) hump = temp;
if (hump < 0) hump = 0 ;
}
/* if we're within the area of a secondary branch */
if ((tt < branchRad) || (tt > (1 - branchRad)))
{
tt = abs(tt-0.5) ; /* because this row is secondary, offset the branches along t*/
temp = sqrt(abs(branchRad*branchRad - (tt-branchRoot)*(tt-branchRoot)))/branchRad; /* roundness */
temp = temp - ((1-cos((ss+0.5)*2*PI)*((1+poleRad)/2))-(-0.5*poleRad+0.5)) ; /* interleave */
if (temp > hump) hump = temp;
if (hump < 0) hump = 0 ;
}
/* if we're within the area of a primary pole */
if (ss > (poleRoot - poleRad) && ss < (poleRoot + poleRad))
{
temp = sqrt(abs(poleRad*poleRad - (poleRoot-ss)*(poleRoot-ss)))/poleRad; /* roundness */
temp = temp * poleRad * 3 ; /* manually increase height cause km, s, radius don't match */
if (temp > hump) hump = temp;
}
/* if we're within the area of a secondary pole */
if ((ss < poleRad) || (ss > (1 - poleRad)))
{
ss = abs(ss-0.5) ;
temp = sqrt(abs(poleRad*poleRad - (ss-poleRoot)*(ss-poleRoot)))/poleRad; /* roundness */
temp = temp * poleRad * 3 ;
if (temp > hump) hump = temp;
}

/* STEP 3 - calculate the new position of the surface point */
/* "P" based on the value of hump */
P = P + n * hump * Km;

/* STEP 4 - calculate the new orientation of the surface normal */
if(UseShadingNormals)
N = normalize(calculatenormal(P)) + diff;
else
N = calculatenormal(P);
}

(return to Studio Pyraxis)